Пирамида Золотого сечения в пансионате Крымские Зори
Человеческий глаз а еще точнее — наш мозг повсюду в природе фиксирует это соотношение, эти пропорции, отмечая их как приятные, красивые, гармоничные. Нам приятно смотреть на произведения классической архитектуры, в которых запроектированы эти волшебные пропорции: такие здания кажутся нам особенно красивыми и гармоничными. То есть форма имеет значение, она оказывает свое влияние на нас, вызывая определенные эмоции, чувство прекрасного.




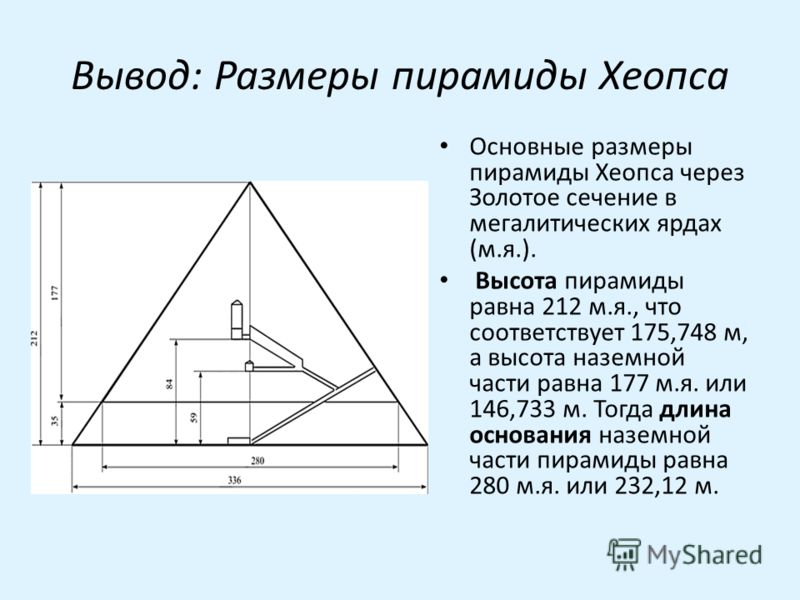
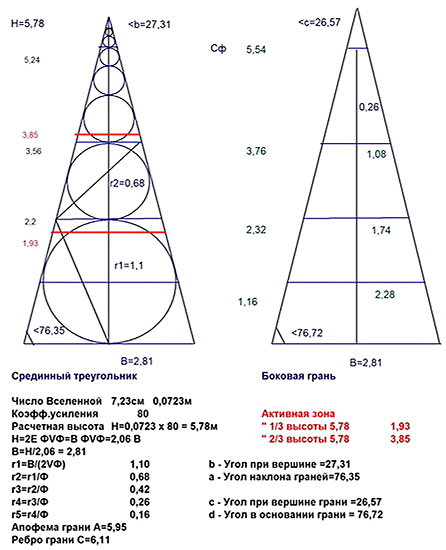
Надо заметить, что это не первые пирамиды на территории России. Более ста лет тому назад граф Львов в своем имении близ города Торжка уже строил пирамиду высотой 11 метров. Геометрические параметры этой пирамиды представляли собой нечто среднее между пирамидами Египта и Пирамидами в пропорциях Золотого Сечения. В этой пирамиде находился винный погреб и вина из него славились в окрестных губерниях. Уже многие тысячелетия форма четырехгранной пирамиды является предметом размышлений для пытливого ума. Хочу обратить внимание на то, что в данном случае мы будем говорить о Пирамидах с конкретной геометрией, основанной на пропорции Золотого Сечения.
- Регистрация Вход.
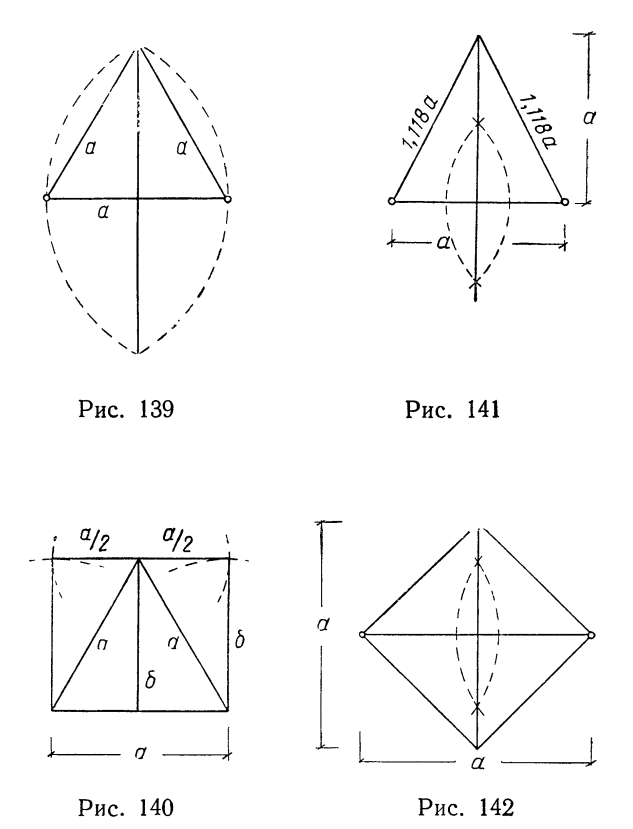
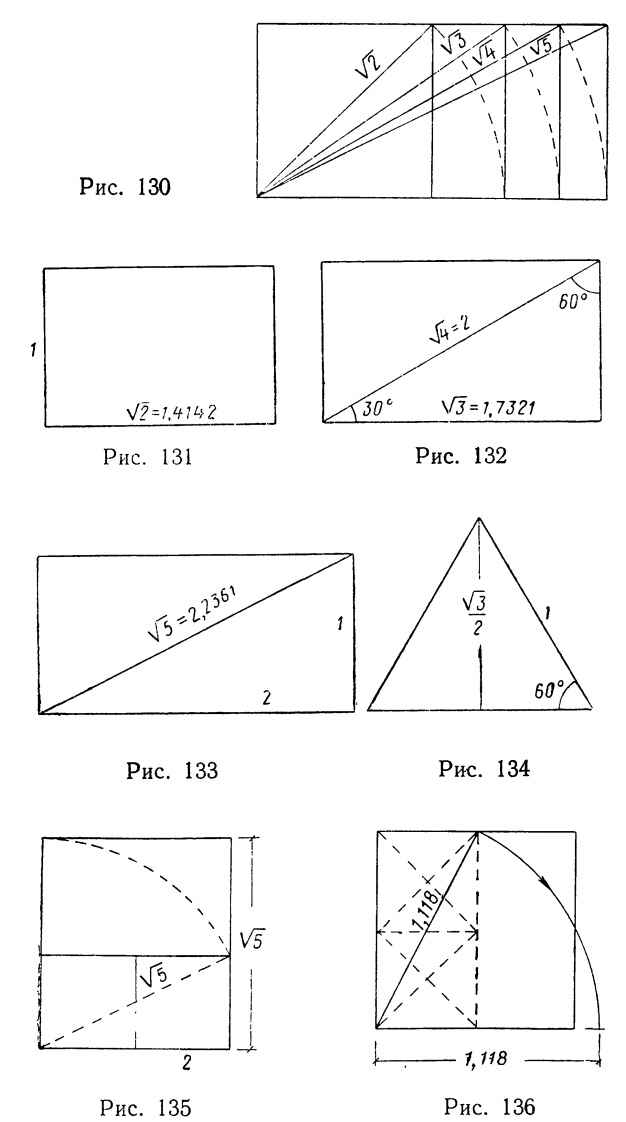
- Чтобы построить любого размера чертеж пирамиды в пропорциях Золотого Сечения надо знать, что это пирамида в которую вписаны стоящие друг на друге сферы. С соотношением диаметров меньшей сферы к большей, примерно, 0.
- Всеобщая история архитектуры.
- Как известно, знаменитое соотношение золотого сечения обнаруживается повсюду в окружающей нас природе и, соответственно, в создаваемых людьми её отражениях — в живописи, архитектуре, скульптуре, технике.
- О пропорции Золотого сечения мы узнали от Леонардо да Винчи, который жил в средние века.
- Effective date :
- Здоровье — это главная ценность жизни, оно занимает самую высокую ступень в иерархии потребностей человека.
- Такие отношения наблюдаются в природе, открыты в науке и соблюдаются в искусстве.
- Регистрация Вход.
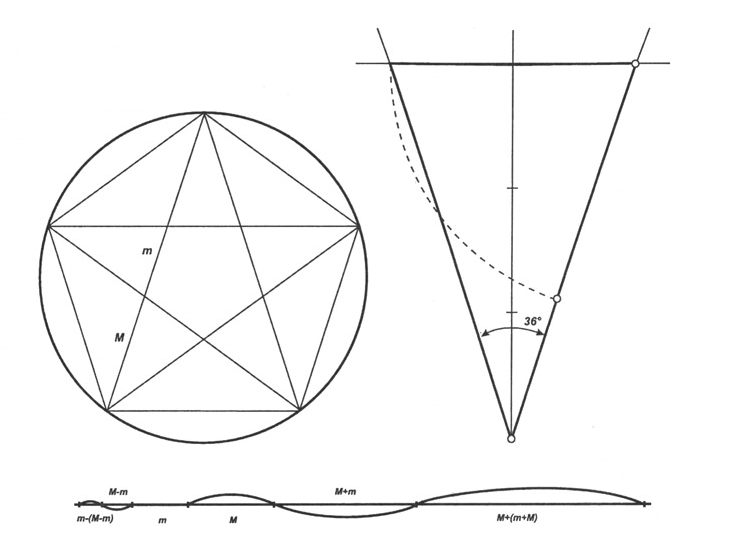
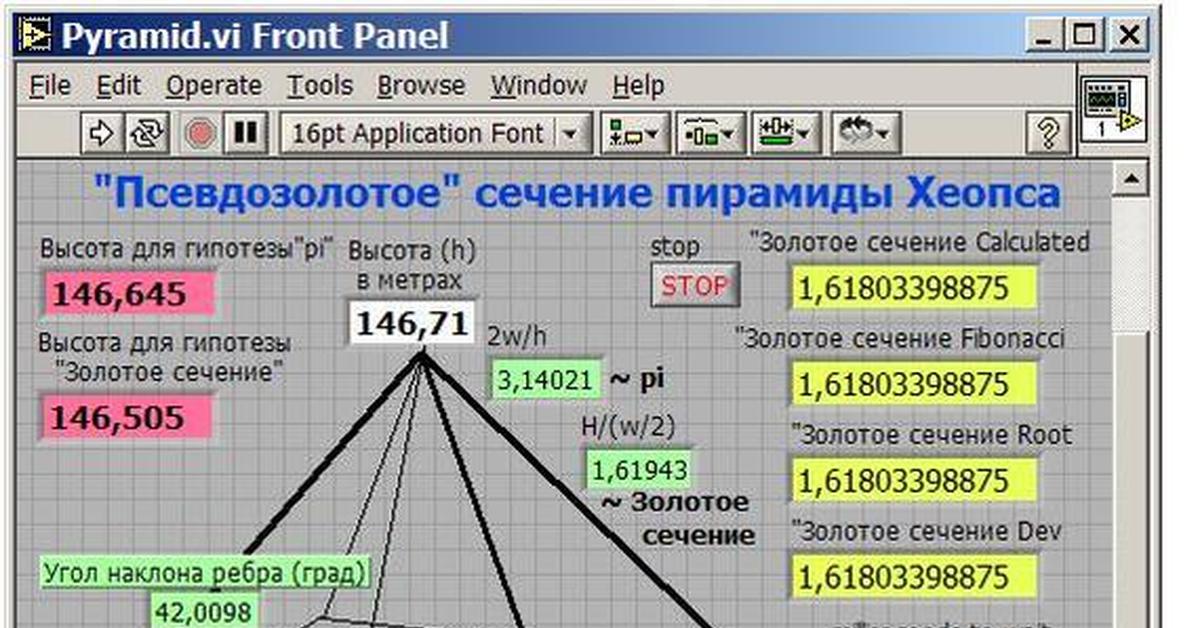



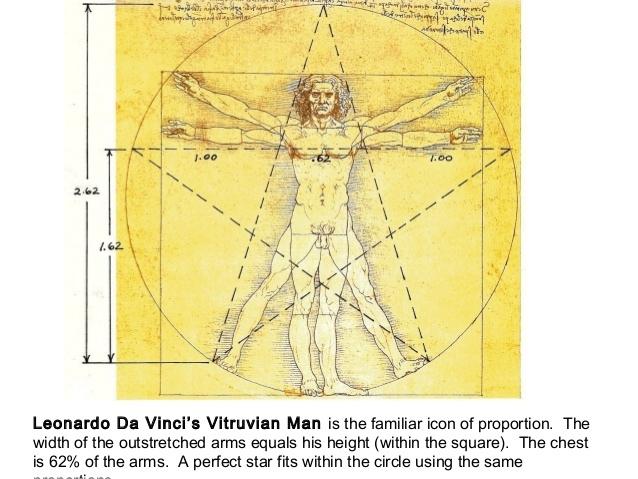
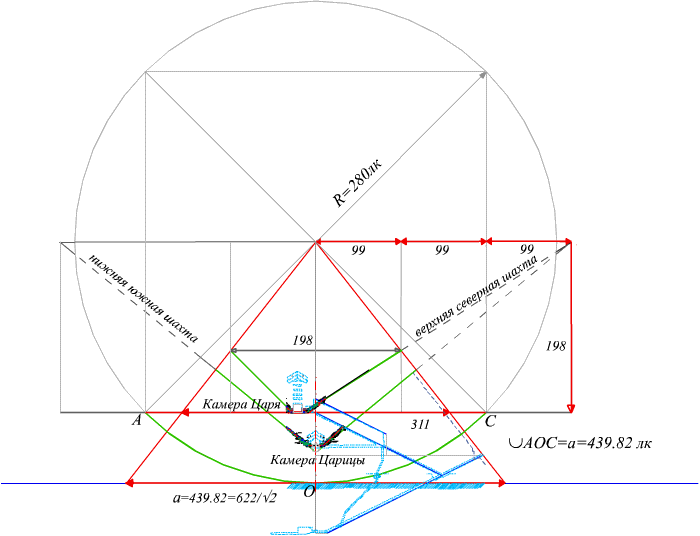



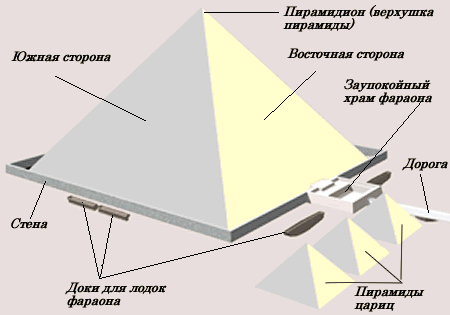


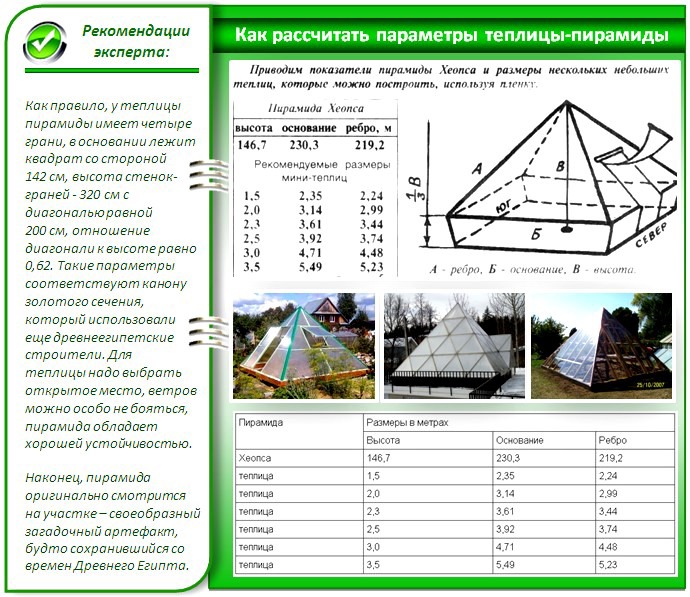
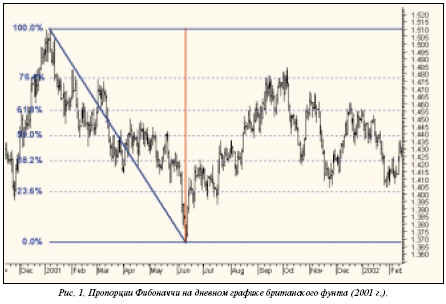
Наверно многие слышали о числе пропорции "Золотого сечения" которое равно 1. Так что особенного в этой пропорции? Если взять числовой ряд Фибоначчи, где каждый следующий член ряда равен сумме двух предыдущих членов ряда, то соотношение двух соседних чисел будет стремиться к пропорции "Золотого сечения". А если построить числовой ряд где каждый член равен не как сумма двух предыдущих чисел а например трех предыдущих чисел то получится уже другая пропорция не совсем золотая, а если суммировать все предыдущие члены для нахождения очередного члена числовой последовательности то мы получим ряд чисел соотношение между соседними числами которого будет равно двум то есть мы получили двоичную систему счета которая используется в компьютерах. Образно систему исчисления можно представить как набор гирек весов для взвешивания не массы а чисел.





Похожие статьи
- Журнальный столик своими руками чертежи размеры - Журнальный стол своими руками: чертежи и конструкц
- Кружево в фотографиях - Ткань золотая парча и новогодние платья из парчи фото
- Выкройка юбки карандаш 54 размера бесплатно - Выкройка юбки. Пошаговые инструкции построения основы
- Коптильни своими руками и размеры